4-min read
As I’ve mentioned previously here, I enjoy gambling. I also love reliving the first time I dove into cryptocurrency and all the scares that came along with the ‘hobby’. Imagine my excitement when I saw both of these together into an online platform.
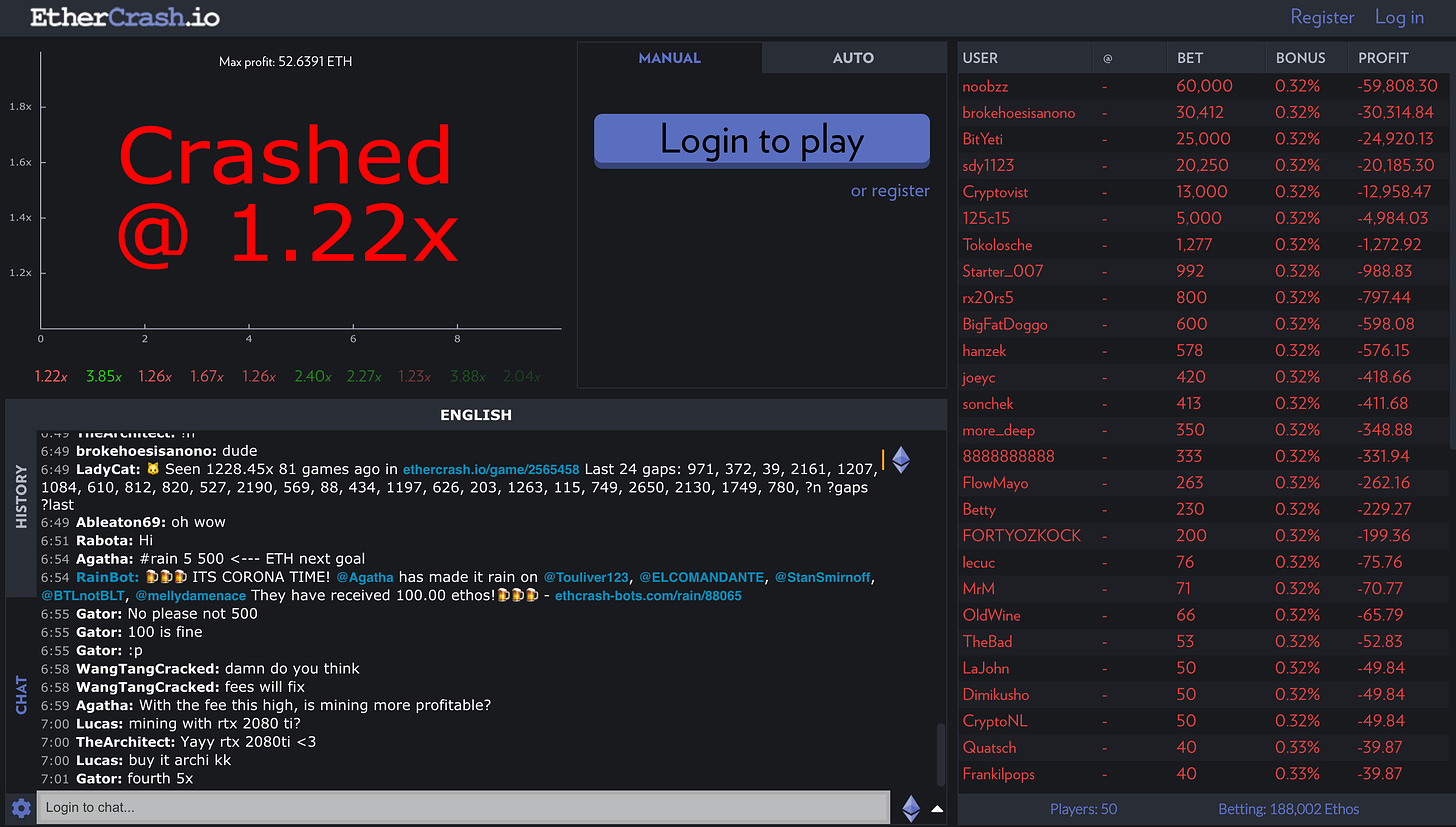
EtherCrash.io is a website where you can hedge real ethos online, by placing bets before the multiplier begins. ‘The Multiplier’ is an exponentially incrementing number that decides the profit you receive. Players have a couple of seconds before the game starts and the graph starts to rise. If you cash out before the multiplier crashes your money is returned with your gain. If you lose, well you lose. On the left, you see the looming graph and previous games. On the right, you can see all the wagers for the current game on the ‘table’ with their respective bet size, bonus percentage, and profit. Similar to all gamified platforms, the design is simple, clean-cut, and gets the point across. But the hook of this addictive platform is placed squarely at the bottom — a chat section where degenerate gamblers can drown their sorrows away or hype up the whales.
At their peak, I could see hundreds of users on this website, and many copycat websites cropping up. It didn’t help YouTube stars were jumping in on this low stakes action and creating catchy titles like, ‘WINNING $300 IN ONE CLICK!’
The website boldly claims the house edge is ‘less than 1.0%.’ I’m going to mathematically prove to you why it’s in your best interest to not use these websites (over the long run).
This particular website doesn't post their code online but allows you to see all previous games. It was trivial to write a scraper to store all game history since the URL incremented along with the games. I grabbed player names, crash value, date, and the number of wagers played per game for further analysis.
Some key takeaways:
Game #1 is missing.
The beta version was launched 2 years ago on Aug 26th, 2018 but only picked up a year later.
The creators of this website were users M1C4A3L and Perchlorate since they were the first to play a handful of games. A keen eye would also tell you this if you looked at the commented out code on the homepage.
The former didn’t play on his own website (don’t get your meat where you get your bread) and the latter managed to lose around 41 Ethereum on the site, or the equivalent of USD$20,000 over 2,539 games. I’m going to make an assumption and say they joined later on as an ‘investor’ to ‘recoup profits.’
Fernandez554 also fits somewhere here in the picture.
At the time of publication, the website has run 2,565,271 games.
Armed with this degenerate dataset, I ran some analysis.
Some Housekeeping
Is the game provably fair or does it at least have some mechanism to prevent the house or player from determining the winning multiplier ahead of time? This term is thrown around a lot, especially with online casino games, so I thought it would be best to test the internal code itself —
function divisible(hash, mod) {
var val = 0;
var o = hash.length % 4;
for (var i = o > 0 ? o - 4 : 0; i < hash.length; i += 4) {
val = ((val << 16) + parseInt(hash.substring(i, i+4), 16))
% mod;
}
return val === 0;
}
function hmac(key, v) {
var hmacHasher = CryptoJS.algo.HMAC.create(
CryptoJS.algo.SHA256, key);
return hmacHasher.finalize(v).toString();
}
function crashPointFromHash(serverSeed) {
var hash = hmac(serverSeed, '0xd8b8a187d5865a733680b4bf4d612afec9c6829285d77f438cd70695fb946801');
// In 1 of 101 games the game crashes instantly.
if (divisible(hash, 101)) return 0;
var h = parseInt(hash.slice(0,52/4),16);
var e = Math.pow(2,52);
return (Math.floor((100 * e - h) / (e - h))/100).toFixed(2);
}Two points:
1/101 games crash instantly, which fits into their narrative of 1% house edge.
If the game doesn’t crash the
crashPointFromHashreturns theMath.floorfunction.
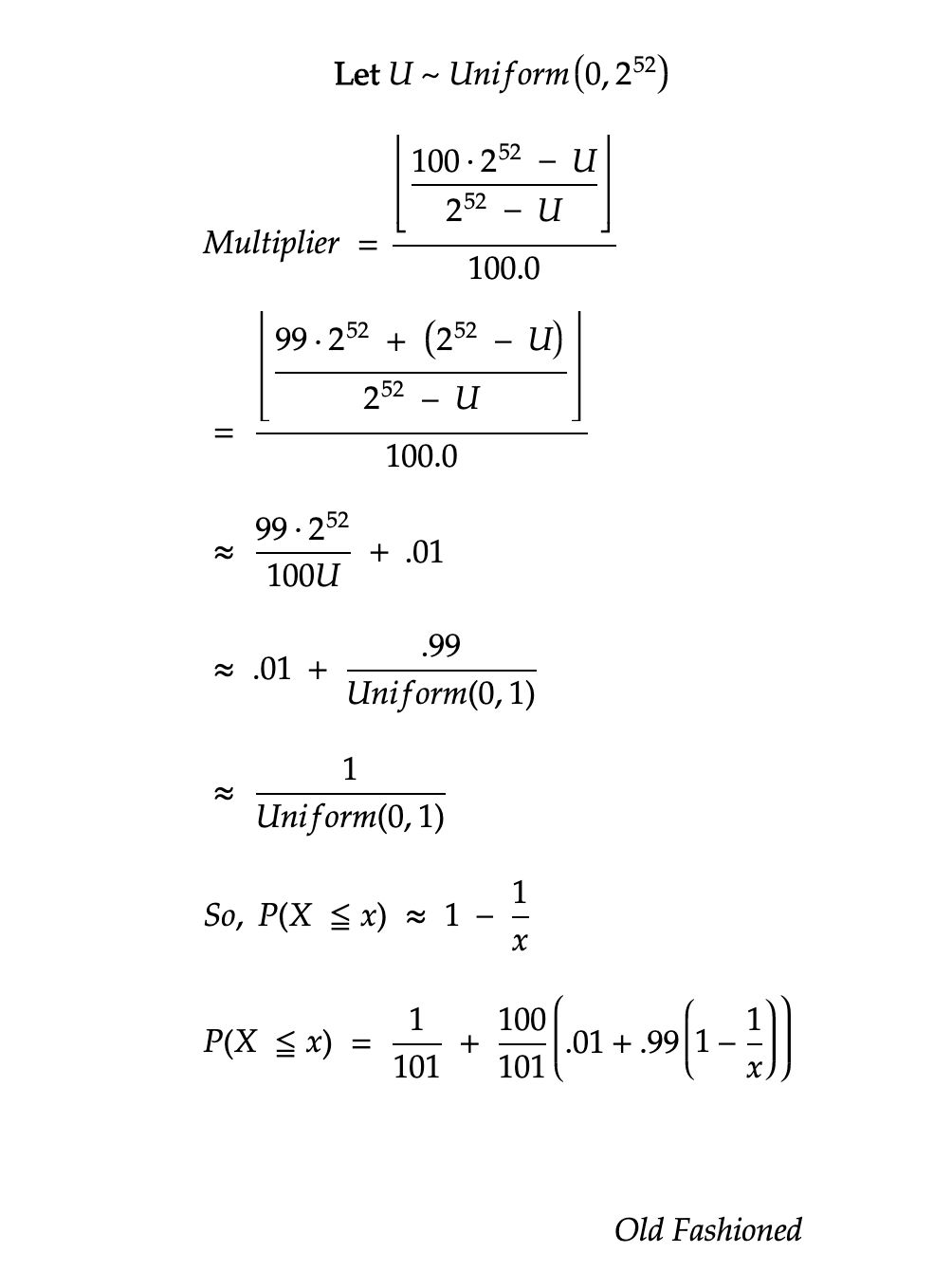
The derivation of the formula is —
Now that we have these two cases figured out, we can find the overall probability that a multiplier is less than or equal to a certain amount. We have a 1% chance the game will crash instantly and a 99% chance it will continue as is. In python, this would look a little like this —
f = 1/101 + (100/101) * (.01 + .99 *(1 - 1 / multiplier))And it seems to be an accurate formula :-)
So an expected value of a $1 wager on Multiplier X would be: the probability of losing into the negative one dollar we would be losing, and sum it with the probability of us winning (which is 1 minus the probability of us losing) and multiply it by the multiplier minus 1.
The expected loss per game nets us a loss of 1 cent. Not much, but the graphs below show a much clearer picture.
Graphs & Stuff
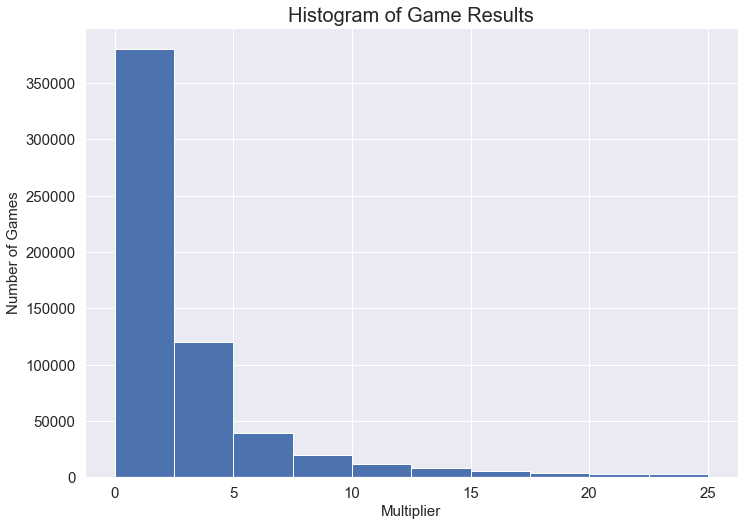
Below is the distribution of game results (multiplier is clipped as to not show outliers and unnecessarily extend the graph). As you can see most games end between 0 and 1, which means the multiplier either crashes or you just about break-even multiplying your wager with nothing.
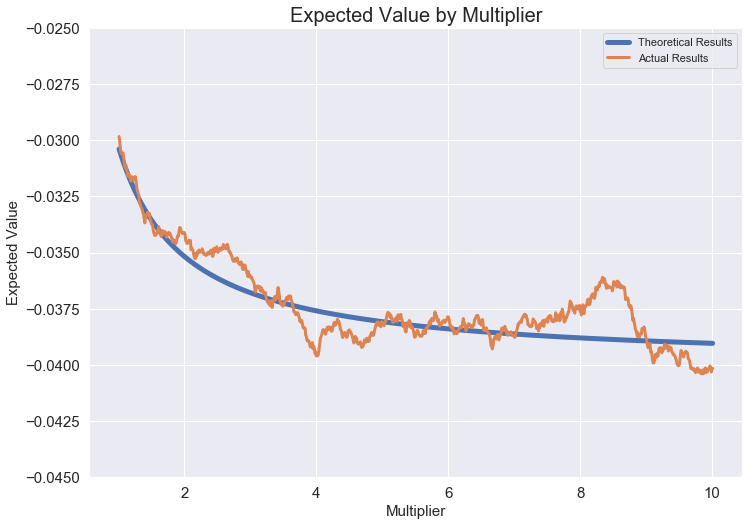
And moment of truth, theoretical results vs. actual results of the games:
The downward trend is indicative of long-term losses and dips the more you ‘wait’ for the multiplier to overextend itself. I wanted to see the winning percentage if I followed the Martingale strategy. It ended up turning in the casino's favor with the probability of losing 1 game in a row closer to 50%, and 10 games in a row ~0.0012%.